SAR Image Compression Based on the Discrete Wavelet Transform*

Zhaohui Zeng and Ian Cumming
Dept. of Electrical and Computer Engineering
The University of British Columbia
Vancouver, BC, Canada V6T 1Z4.

ABSTRACT: --- SAR image compression is very important in reducing the costs of data storage and transmission in relatively slow channels. In this paper, we propose a compression scheme driven by texture analysis, image segmentation and speckle noise reduction within the wavelet framework. The result is favourable compared to the conventional zero-tree wavelet compression method.

* Presented at the Fourth International Conference on Signal Processing ICSP'98, Beijing, China, October 12-16, 1998.     

1.     Introduction

Synthetic aperture radar (SAR) data represents an important source of information for a large variety of scientists around the world. However, while the volume of data collected is increasing rapidly, the ability to transmit it to the ground, or to store it, is not increasing as fast. Also, while storage densities on archiving media are improving with technological developments, our ability to generate new data is increasing even faster. Thus, there is a strong interest in developing data encoding and decoding algorithms which can obtain higher compression ratios while keeping image quality to an acceptable level.

There are some special characteristics to SAR imagery which affect the design of an image compression algorithm. The first is the speckle phenomena which results from the coherent radiation. A fully developed speckle pattern appears chaotic and unordered, and severely degrades the quality of SAR images. The second is that there is rich texture information and large homogeneous regions in SAR images. This makes it natural to consider a way to reduce coding bits within homogeneous regions of terrain. The third is that very high dynamic range of SAR image data is unlike those of image data from other sensors, such as optical sensors. These differences mean that encoding/decoding algorithms designed for optical data may not be appropriate for SAR data.

Wavelet transforms have received significant attention because their multi-resolution decomposition allows efficient image analysis. It has been used in analysis, noise reduction and data compression of SAR images [1]. Thus, using the discrete wavelet transform (DWT), the procedures of terrain segmentation, speckle noise reduction and data compression can be efficiently combined in a single process of decomposition and reconstruction. In this work, we will develop an algorithm using tree-structured texture analysis, soft-thresholding speckle reduction, quadtree homogeneous decomposition, and modified zero-tree coding scheme. The result is compared to the conventional zero-tree wavelet transform scheme and shows that our method is very promising method for practical use.  

2.     Texture Analysis with Tree-Structured Wavelet Transform

Using the DWT, every coefficient at a given scale can be related to a set of coefficients at the next finer scale of similar orientation. The coefficient at the coarse scale is called the parent, and all coefficients corresponding to the same spatial location at the next finer scale of similar orientation are called children. For a given parent, the set of all coefficients at all finer scales of similar orientation corresponding to the same location are called descendants.

The traditional pyramid-type wavelet transform recursively decomposed subsignals in the low frequency channels. However, since the most significant information of a texture often appears in the middle frequency channels, further decomposition just in the lower frequency region, such as the conventional wavelet transform does, may not help much for SAR image which contains rich texture information. Thus, an appropriate way to perform the wavelet transform for textures is to detect the significant frequency channels and then to decompose them further.

Here, we approach this problem by analyzing SAR images by the tree-structured wavelet transform used in [3]. The key point is that the decomposition is no longer simply applied to the low frequency subsignals recursively. Instead, it can be applied to the output of any filter hLL, hLH, hHL or hHH. It can be described as the following:

  1. Decompose a given textured image with 2-D two scale wavelet transform into 4 subimages, which can be viewed as the parent and children nodes in a tree.

  2. Calculate the energy of each decomposed image (children node). That is, if the decomposed image is x(m,n), with 1 <= m <= M and 1 <= n <= N, the energy is:

    3.  
            e  =  1/(MN)    SUM(i=1,M)  SUM(j=1,N)   |x(m,n)|(1)
     
  3. If the energy of a subimage is significantly smaller than others, we stop the decomposition in this region since it contains less information. This step can be achieved by comparing the energy with the largest energy value in the same scale. That is, if  e < C e max, stop decomposing this region where C  is a constant less than 1.

  4. If the energy of a subimage is significantly larger, we apply the above decomposition procedure to the subimage.
This method is analogous to computing the complete wavelet packet transform to a certain maximum level, then pruning the branch from top to bottom using the above energy threshold. The texture factors are created after this step. It is represented as a series of constants  {F1, F2, ... , Fl, ...}  which corresponds to a series of frequency channels.  Fl  is a constant between (0 - 1). In a frequency channel with more texture, Fl  is smaller; in a channel with less texture, Fl  is larger.  

3.     Homogeneity Map

An image map which specifies the degree of homogeneity can be helpful in achieving higher compression gain because we can allocate fewer bits to homogeneous regions while allocating more bits to those regions containing more detail and sharp features. Here, we apply a very simple segmentation scheme based on quadtree decomposition of the image at the lowest scale. Quadtree decomposition is an analysis technique that involves subdividing an image into blocks that are more homogeneous than the image itself. It starts at decomposing the whole image into four equal sized blocks, and then testing each block to see if it meets some criterion of homogeneity (e.g. if all the pixels in the block are within a specific dynamic range). If a block meets the criterion, it is not divided any further. If it does not meet the criterion, it is subdivided again into four blocks, and the test criterion is applied to those blocks. This process is repeated iteratively until each block meets the criterion.

After quadtree decomposition, we get two lists: a homogeneous list and a target list. The homogeneous list consists of the relatively homogeneous regions. Each homogeneous region is represented by the coordinates of the pixel at the left up corner and the size of the region. The target list consists of those single component regions, represented by their coordinates. The test criterion we choose is to split a block if the maximum of the block elements minus the minimum value of the block elements is greater than the threshold th.

 th   =   g s h                                                                             (2)
where  sh  is the standard deviation of the wavelet coefficients at the highest frequency band in the diagonal direction, and  g  is a selected constant.  

4.     Speckle Reduction

Speckle noise is modeled as multiplicative noise. After logarithmic transform, the multiplicative noise become additive noise. The discrete wavelet transform is a linear transform and the speckle noise is still additive in the wavelet domain. A soft threshold [2] is applied to all the wavelet coefficients except those of the lowest scale. This removes some of the speckle inherent in SAR imagery while preserving much of the detail, thus improving compression performance. The value of the threshold   tl   is given by the formula:
 tl  =  Fl sl  sqrt{ 2 log(nl) }                                                  (3)
where  nl  is the number of pixels in each frequency band,  sl  is the same as  sh , and  Fl  is the feature factor at the corresponding frequency channel. 

5.     Modified SPIHT Coding Scheme

The embedded zerotree coding (EZW) [4] is a very effective and computationally simple technique for image compression. The "set partitioning in hierarchical trees'' method (SPIHT) [5] improves the performance of EZW based on three concepts:
  1. partial ordering of the transformed image elements by magnitude, with transmission of order by a subset partitioning algorithm that is duplicated at the decoder,

  2. ordered bit plane transmission of refinement bits, and

  3. exploitation of the self-similarity of the image wavelet transform across different scales.
Here, we modify the SPIHT by soft-thresholding, homogeneous map, and feature factors so that it is more appropriate for SAR images.

A wavelet coefficient  x  is said to be insignificant with respect to a given threshold  T  if  |x| < T.  The zerotree structure is based on the hypothesis that if a wavelet coefficient at a coarse scale is insignificant with respect to a given threshold T, then all wavelet coefficients of the same orientation in the same spatial location at finer scales are likely to be insignificant with respect to T. In the progressive transmission mode, the nth bit of the wavelet coefficients is transmitted if  2n  <=  |ci,j|  <   2n+1. To make clear the relationship between magnitude comparisons and message bits, we use the following function to indicate the significance of a set of coordinates t.

Sn(t)  =  1     if  max{ |ci,j| }  >=  2n,   (i,j)  Π t
           =  0    otherwise. (4)
 
Our method is different from the conventional EZW or SPIHT methods in the following ways:
  1. A different parent may have the same children because the tree-structured wavelet transform allows the size of children to be smaller than that of the parent, which is unlike the pyramid structure used in the SPIHT method. For example in Figure 1, the coefficient in the scale branch (3,2) has descendants in (3,8), (3,9), (3,10), (3,11), (2,8), (2,9), (2,10), (2,11).

  2. If the descendants have more than one parent, they are regarded as significant once they satisfy the condition of the threshold  Ti  from any one of their parents f; the descendants are insignificant only when they satisfy the condition of the thresholds { T1, T2, ... , Ti } from all of their parents.

  3. The condition of  Sn  is changed to be  max{ |ci,j| }  >=  Fl 2n ,   (i,j)  Π t,  where Fl is a texture factor. Thus, texture information has the higher priority in bit allocation.

  4. Two different coding lists, the homogeneous list and target list, are encoded separately.

6.     New Encoding Scheme

Because the homogeneity map of the lowest scale has been created by the quadtree decomposition, we can reduce the number of bits by encoding the homogeneity map while allocating more bits to highlighting areas of greater detail. To further improve the coding efficiency, the soft-thresholding is applied before the start of coding at other scales. The residual from soft-thresholding and coding is kept and then losslessly compressed using arithmetic coding and transmitted to decoder based on the users' demand.

The features of the new method are:

  • Speckle reduction:   Soft thresholding is applied to all wavelet coefficients except the lowest scale ones. After quantization, the length of significant bits of wavelet coefficients is shortened. The residual part is kept and transmitted based on user's demands.

  • Encoding homogeneous map:   To the components in the homogeneous list, we send the decoder the average value, the dynamic range and the size of the homogeneous region, and then use this average value as the threshold to decide the significant coefficients at the next finer scale. Then we compute the difference between the value of every component in the homogeneous region and the average value. We quantize these differences and transmit them based on the bit plane.

  • Tree-structured coding:   The wavelet coefficients in the target list are quantized and transmitted based on the algorithm used in the modified SPIHT algorithm. At every scale branch, three candidate encoding schemes will be tested: raw data, arithmetic coding, and run-length coding. The candidate with the best performance is chosen as the encoding scheme at this scale branch.

  • Residual coding:   Efficient compression of these residuals is essential to the efficiency of the algorithm as a whole. Because this part of the coefficients possess a rapidly decaying exponential distribution with a maximal number of zero coefficients. This skewed distribution makes arithmetic coding the best choice for lossless compression.

7.     Experimental Results

The experimental data we choose is X-band high-resolution airborne 1-look SAR image showing part of Bedfordshire in south-east England Figure 2. It displays many of the features that typically appear in airborne imagery. In our experiments, Daubechies 4 (DB4) wavelet transforms (quadrature mirror filter pairs) are employed.

The tree structure analysis is illustrated in Figure 1. Three level decomposition happen in three places: the lowest scale channel, the lower vertical scale channel, and the highest diagonal direction. The compression result is shown in Figure 3 (0.1 bits/pixel), Figure 4 (0.2 bits/pixel), and Figure 5 (0.2 bits/pixel) with conventional EZW. From those images, we can see that this algorithm works well on airborne SAR image and outperforms the conventional wavelet method.


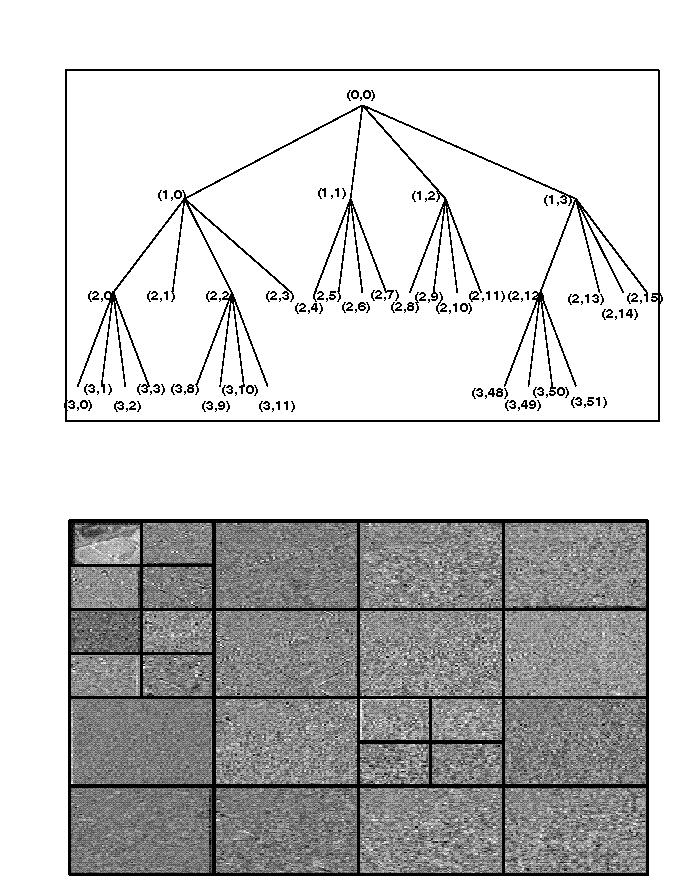
Figure 1: Tree-structured analysis.

   
   Figure 2: Original SAR image.
 
 		    Figure 3:  0.1 bits/pixel 
 
 
  
   Figure 4: 0.2 bits/pixel     Figure 5: 0.2 bits/pixel with EZW 

8.     Conclusions

We have presented an algorithm that operates through the combination of image analysis, speckle reduction, and image compression and accomplishes embedded coding. It is more effective than the conventional zerotree algorithm. The performance of this coding scheme can also be improved by choosing more appropriate image analysis tools, and coding sequence based on the analysis result.   

References

  1. D. Wei, H. Guo, J. Odegard, M. Lang and C. Burrus, "Simultaneous Speckle Reduction and Data Compression Using Best Wavelet Packet Bases with Applications to SAR based ATD/R", In SPIE Conference on Wavelet Applications, Vol. 2491, Orlando, FL, April 1995.

  2. D. Donoho, "De-Noising by Soft-Thresholding", IEEE Trans. Information Theory, Vol. IT-41, pp. 613-627, May 1995.

  3. T. Chang and C. Kuo, "Texture Analysis and Classification with Tree-Structured Wavelet Transform", IEEE Trans. Image Processing, Vol. 2, No. 4, pp. 429-441, October 1993.

  4. J. Shapiro, "Embedded Image Coding Using Zerotrees of Wavelet Coefficients", IEEE Trans. Signal Processing, Vol. 41, pp. 3445-3462, 1993.

  5. A. Said and W. Pearlman, "A New, Fast and Efficient Image CODEC Based on Set Partitioning in Hierarchical Trees", IEEE Trans. Circuits and Systems for Video Technology, Vol. 6, pp. 243-250, 1996.