
|
|
Ian Cumming, and Wei Xu |
Radar Remote Sensing Group (RRSG), Dept. of Electrical & Computer Engineering, University of British Columbia, 2356 Main Mall, Vancouver, BC, Canada V6T 1Z4 http://www.ee.ubc.ca/sar/ | |
Contents
In this paper, we present a comparison of the phase unwrapping of the noisy Sardegna interferogram between the new region-growing algorithm and two of the most widely-used phase unwrapping algorithms: the cut-line algorithm and the weighted least squares algorithm, by verifying the unwrapped phase with topographic map data.
The verification and comparison show that the region-growing algorithm unwraps more of the low-coherence areas successfully, and makes fewer ambiguity errors than the other two algorithms.
Keywords: Phase unwrapping, Region-growing, Cut-line, Weighted least squares, DEM
Phase unwrapping has been a difficult step in interferometric SAR processing. A number of phase unwrapping algorithms for SAR interferograms have been proposed. However, none of the existing phase unwrapping algorithms give satisfactory results when noisy and/or dense fringes occur. We have developed a new region-growing phase unwrapping algorithm, which can cope with very noisy interferograms [1,2]. The verification of the unwrapped phase of the noisy Sardegna interferogram will help to compare the performance of the algorithms.
The success of phase unwrapping algorithms often depends upon the path selected to perform the unwrapping, or the lack of a path. In the region growing algorithm, better performance is sought by dynamically adjusting the unwrapping path according to local noise and phase continuity conditions. The algorithm is also able to correct unwrapping errors to a certain extent, and to stop their propagation. The algorithm achieves these goals in the following way:
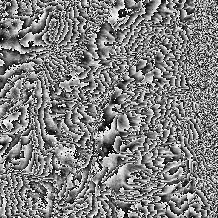
The ERS-1 data of Sardegna, Italy, collected on August 2, 1991 (orbit 241) and August 8, 1991 (orbit 327) with 126 m perpendicular baseline was used to test the unwrapping algorithms. A 16 km square portion of frame 801 was used, centered at 40 degrees 8 minutes North and 9 degrees 32 minutes East, and situated towards the far range of the full scene. The interferogram was formed, smoothed to square pixels, and roughly flattened. The phase and local coherence of the 512 x 512 pixel interferogram are shown in Fig. 1.


|
This SAR interferogram is considered to be difficult to unwrap because of its large areas of low coherence, which are mainly caused by layover due to the extreme local topography. These areas of low coherence segment the interferogram into many pieces, which creates structural difficulties for the unwrapping algorithms [2].
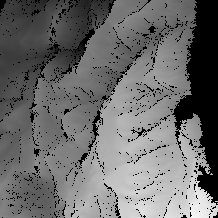
The Sardegna interferogram was unwrapped using the region-growing (RG) algorithm with typical quality control parameters . The phase of the largest unwrapped region is shown in Fig. 2. The algorithm automatically recognizes that the low-coherence sea area on the right side should not be unwrapped. The low-coherence regions caused by layover in the land area are prominent in the figure as they are left wrapped, although small isolated unwrapped areas may be present in some of the black areas.
|
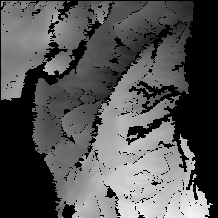
Unwrapping using the "cut-line" (CL) algorithm was implemented by Dr. Ian Joughin of JPL [3], using a modified version of the original CL algorithm [4]. The phase of the largest unwrapped region is shown in Fig. 3a. Again the sea area is not unwrapped. However, the CL algorithm has not been able to merge a large area in the bottom left of the interferogram (shown black in Fig. 3a) into the main unwrapped area.
The unwrapping using the "weighted least squares" (WLS) algorithm was implemented at DLR [5], and the resulting unwrapped phase is shown in Fig. 3b. The WLS algorithm gives a result which is pleasing in appearance because of its completeness and smoothness, but it is clear that misleading results are obtained in the sea area and in places of sharp topography.

|
Although the three algorithms agree well in some regions, there are many parts of the interferogram where the unwrapping results disagree substantially. In these cases, ground truth can be used to understand and resolve the differences, thereby helping to evaluate the unwrapping quality of the three algorithms. As accurate digital elevation model (DEM) data for the whole interferogram was not available to us, elevation data from a 1:25,000 topographic map for 5 range lines are used to compare the algorithms.
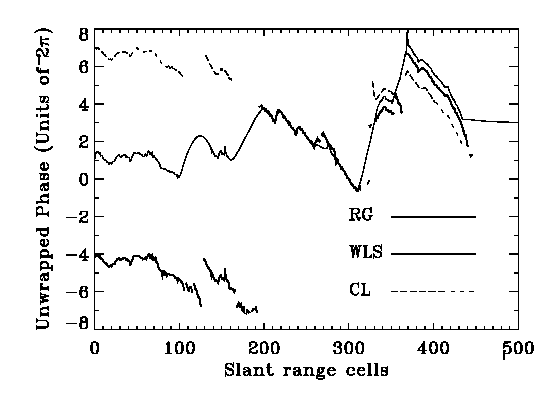
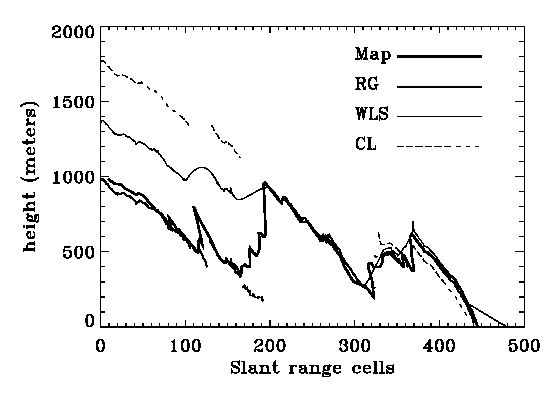
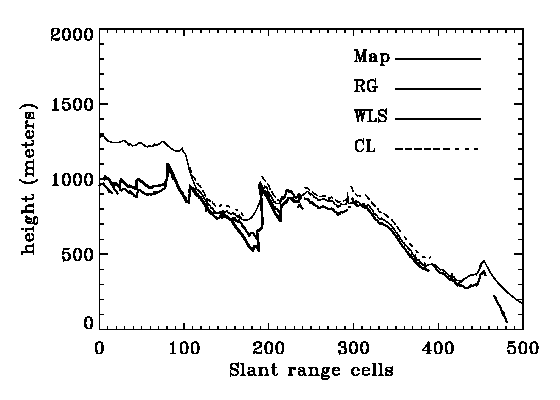
Range line 127 (see Fig. 2) is chosen as a representative range line because all three algorithms unwrapped most of the pixels on this line, and challenging topographic features are present. As the interferogram is not accurately flattened, it is useful to begin by comparing the unwrapped phase of the three algorithms. This is a fair comparison because the imperfect flattening affects the results of each algorithm equally. The comparison of phases is shown in Fig. 4a. Gaps in the RG and CL curves indicate where the phase values are not unwrapped (or are unwrapped into unjoined regions).
The following observations can be made for each group of range cells (RC) in Fig. 4a:
|
|
In Fig. 4a, the fine structure of the phase of the three results agree reasonably well, but major differences exist in the ambiguity levels. The map elevations will be used to identify which of these solutions is best.
To verify the unwrapped phase values, they were converted to elevation values and then compared to the elevation data from the maps. The elevation data was read from the 1:25,000 topographic maps in the ground range domain and then converted to the slant range domain.
After using map data to refine the interferogram flattening, the phase-derived elevations are compared with the map elevations in Fig. 4b. One ambiguity of 2 corresponds to about 70 m of elevation change with this 126 m baseline.
From the comparison in Fig. 4b, the following observations can be made:
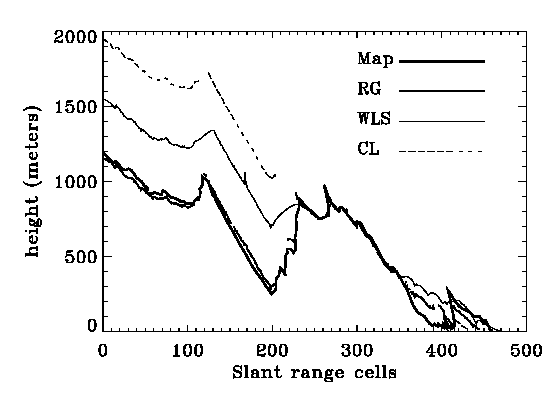
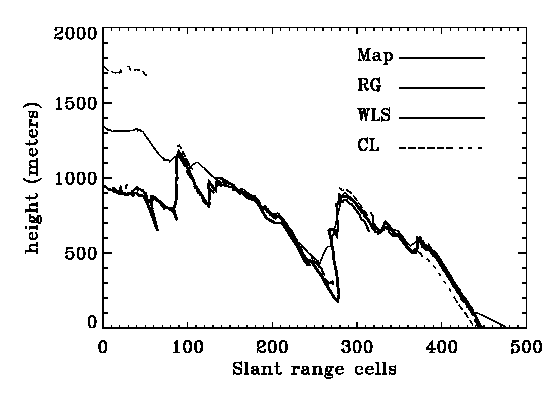
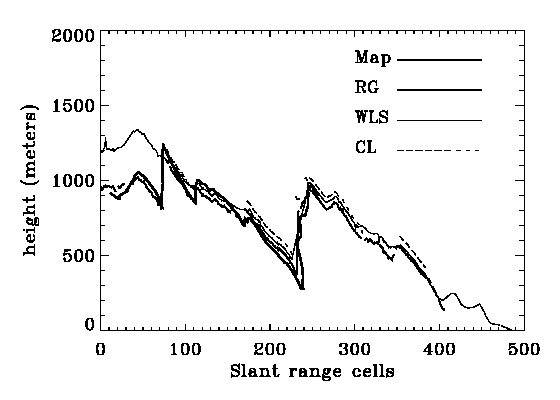
The other range lines chosen for verification are line 63, line 191, line 255, and line 383 as shown in Fig. 2. Fewer lines are chosen near the bottom because DEM values are only available on the near range side there.
The comparison of phase-derived elevations with the map elevations for these lines are shown in Fig. 5.
|
|
|
|
Although errors in the map elevations within one ambiguity exist, as the purpose of the verification is to show the correct ambiguity rather than to measure the exact error of the InSAR derived heights, the accuracy of the map derived heights is sufficient. The RMS differences to the map elevations are shown below in Tab. 1.
| Range Line Number | 63 | 127 | 191 | 255 | 383 |
|---|---|---|---|---|---|
| RG vs. Map | 54 | 96* | 52 | 51 | 45 |
| WLS vs. Map | 281 | 256 | 169 | 159 | 182 |
| CL vs. Map | 542 | 473 | 271 | 105** | 87** |
From Fig. 5 and the table values, the following observations can be made.
On the left side of the image where large differences exists among the three algorithms, the RG algorithm provides the correct ambiguity in most areas with errors of only one ambiguity in other areas. In contrast, the WLS algorithm shows large errors of about 5 ambiguity levels, and the CL algorithm shows the largest errors of about 10 ambiguity levels in the top lines where unwrapped phase is available or is not able to provide the unwrapped phase. In the remainder of the area where the difference between the algorithms is generally within one ambiguity.
The error from the RG algorithm is generally with one ambiguity RMS, which is partly caused by the inaccuracy of the map elevations, except in the line 127 where unwrapping around RC 190-192 proceeds from the facing slope while the regular spaced map elevations take the value from the back slope and cause about 400 m additional error. The WLS algorithm is with 2-4 ambiguities RMS. The CL algorithm is generally with 4-8 ambiguities RMS, except in the line 255 and 383 where unwrapping in the difficult area are not provided and the error looked smaller.
The observations from the additional range lines are in general agreement with the observations from the representative range line.
In the comparison with map data, the RG algorithm has proven to be less susceptible to large errors that can occur in noisy areas of the interferogram. This is largely because of the ability of the RG algorithm to venture deeper into noisy regions, attempting to work its way through from many different directions and stop unwrapping from unreliable directions. Therefore, the comparison illustrates the effectiveness of the region growing algorithm in unwrapping difficult areas.
In the authors opinion, the CL algorithm results in unwrapping errors because it cannot avoid linking the wrong pairs of residues when the residue density is high. Also, the WLS algorithm results in unwrapping errors because it tries to fit the unwrapped phases to a smooth model in low-coherence areas, which is not valid in areas of significant topographic changes.
As the 5 lines examined spans the interferogram from the top to bottom, our observations above will likely apply to other areas of the interferogram.
With the help of 1:25,000 topographic maps, the unwrapped phase of the Sardegna interferogram has been verified along a representative set of range lines. In the verification, the region-growing phase unwrapping algorithm was compared with two of the most popular algorithms available. The Sardegna interferogram was used for the comparison, because it has extreme topography, which has caused problems for many other phase unwrapping algorithms. It has been shown that the region-growing algorithm can successfully unwrap further into the low-coherence regions than the other two algorithms, and makes fewer ambiguity-level errors. This is because of its ability to work across and around low-coherence regions, which results in more accurate connecting of the high-coherence regions. This results in a higher proportion of the interferogram being unwrapped, and more regions being joined into one contiguous region.
The authors would like thank Dr. Ian Joughin of the Jet Propulsion Laboratory for unwrapping the Sardegna data using the "cut-line" algorithm and Dr. Marcus Schwaebisch of the German Aerospace Research Establishment (DLR) for the unwrapping using the "weighted least squares" algorithm.