sandora@ee.ubc.ca ianc@ee.ubc.ca

Presented at the 13th International Conference on Digital Signal Processing, Santorini, Greece, July 2-4, 1997. Published on pages 337-340 of the proceedings.

ABSTRACT

The momentary Fourier transform (MFT) computes the DFT of a discrete-time sequence for every new sample of the sequence. It has an efficient recursive form, and an alternate derivation is given using matrix transformations. Recursive and non-recursive forms of the inverse MFT are also given, which can provide efficient frequency domain filtering.

CONTENTS

1 INTRODUCTION

The momentary or moving Fourier transform (MFT) is a method of computing the discrete Fourier transform (DFT) of a sequence in incremental steps. It can be computed using an efficient recursive formula, and it is useful in cases where the detailed evolution of the spectra of a time series is wanted, and in cases where only a few Fourier coefficients are needed.

Uses of the incremental DFT were introduced by Papoulis in 1977 [1], and by Bitmead and Anderson in 1981 [2]. A detailed derivation of the momentary Fourier transform was given by Dudás in 1986 [3]. In 1991, Lilly gives a similar derivation, using the term "moving Fourier transform", and uses the MFT for updating the model of a time-varying system [4].

In this paper, we introduce the matrix form of the momentary transform in Section 2, and show that it has a recursive form. In Section 3, we show that when the momentary matrix transform takes the form of the discrete Fourier transform, the resulting MFT has an efficient (recursive) computational structure. In Section 4, the inverse MFT is derived for the first time. An example of the use of the MFT and a discussion of its computational efficiency is given in Section 5.

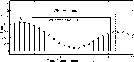
Let x_i be a sample of an arbitrary discrete-time function of one variable. The function will be analyzed through an N-point window, ending at the current time i. In subsequent analyses, the window will be advanced one sample at a time, as shown in Figure 1.

Figure 1: The sampled function x_i

At times i-1 and i, the windowed samples can be represented by the column vectors:

, (1)

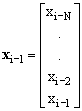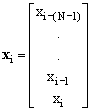
Let T be an N´N non-singular transformation matrix, which has the inverse T^-1. The sequence of windowed vectors can be transformed by T:

y_i-1 = Tx_i-1 , y_i = Tx_i , . . . (2)

Let P be an N´ N elementary cyclic permutational matrix:

(3)

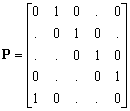
When the vector x_i-1 is premultiplying by P, a one-element circular shift is performed, such that the time index of each element is increased by one, and the first element becomes the last one:

(4)

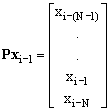
Then the x_i vector can be expressed by the shifted x_i-1 vector, with an adjustment D_i made for the samples entering and leaving the window:

(5, 6)

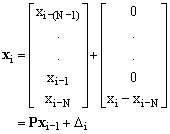
The transformation TP will be called the momentary matrix transform (MMT) because it represents the matrix transform T shifted one moment (i.e. one sample) in time.

Substituting (6) into the transformation associated with the i^th window in (2), the following relationships are obtained:

(7, 8)

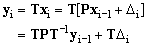
where use is made of the inverse transform x_i-1 = T^-1 y_i-1.

Equation (8) expresses the recursivity of the momentary matrix transforms, since calculation of the newly transformed index vector y_i needs the previously transformed index vector y_i-1 and the difference between the function values of the samples entering and leaving the window. The MMT is particularly efficient if the similarity matrix P'=TPT^-1 is diagonal.

3 MOMENTARY FOURIER TRANSFORM

An interesting case is when the matrix transform T performs the Discrete Fourier Transform (DFT). When

W^k = e^{-j2 p k/N} , k = 0, 1, 2, . . ., N - 1 (9)

are the N complex roots of unity (the DFT twiddle factors), the DFT can be written as the matrix transform:

(10)

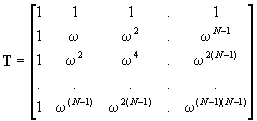
and the inverse DFT is implemented by the matrix transform:

(11)

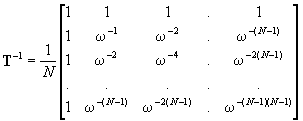
It can be shown that the similarity transform has the desired diagonal form:

(12)

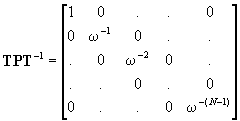
so that the momentary Fourier transform (MFT) has the efficient recursive form:

(13)

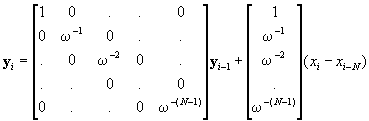
To get (13), note that , which means that:

(14)

It can be shown that the DFT is the only matrix transformation which possesses the diagonal form (12).

The N-element vector y_i contains the Fourier coefficients of the N-point sequence x_i ending at time i. Note that while the vectors x_i-1 and x_i share N-2 common elements, the vectors y_i-1 and y_i share no common elements in general.

Note also that in the incremental form (13), each spectral component y_i,k at time i is computed only from the same spectral component at time i-1,

(15)

so that the recursive formula is particularly efficient if only a few frequency components need to be computed, as in the zoom transform.

Thus we see that if the DFT of the sequence [x_i-N…x_i-1] has been computed, the DFT of the sequence [x_i-N+1…x_i] can be computed using N complex multiplies and N+1 complex adds (the obvious computational savings are available if the time sequence is real-valued). Because of the diagonal structure of TPT^-1, the MFT can also be efficiently computed for shifts q>1 [4], but its efficiency drops relative to the FFT, as the computation load is O(qN) (see Section 5.2).

4 THE INVERSE MFT

The matrix transformation equations lead to an efficient recursive implementation of the inverse momentary Fourier transform as well. Starting with the matrix form of the inverse DFT:

(16)

note that for a recursive calculation, only the last element of x_i need be calculated at the current time. This involves only the last row of the matrix T^-1 in (11) so that:

(17)

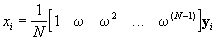
and the obvious recursion exists:

(18)

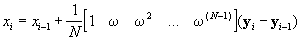
This recursion requires N complex multiplies and N+1 complex adds for each new output point.

Note also that in the non-recursive form (16), the oldest element of x_i, can be computed using adds only:

(19)

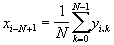
from which the sequence x_i can be computed from the 2-dimensional "sequence" y_i with an N-1 sample delay. In this way the MFT/IMFT combination (15),(19) can provide an efficient frequency-domain filter, especially if many of the DFT coefficients are set to zero by the filtering operation.

5 USAGE OF THE MFT

To illustrate the usage of the incremental form of the MFT, a complex exponential of length 3N samples is used. Using an analysis record length of N = 30, and a frequency of 20 cycles/record, the magnitude of the evolving spectrum is shown in Figure 2, when the MFT is incremented by one sample at each analysis stage.

Figure 2: Illustration of MFT usage

The MFT begins with the initial conditions of y₀ = 0. This is equivalent to having N zeros precede the data vector. In Figure 2, note how the energy in the spectrum rises from zero to a maximum in the first N samples. Also note how spectral leakage is observed in the first N-1 time samples, because the complex exponential does not have an integer number of cycles/record over this time. After time N-1, there is an integer number of cycles/record, so all the energy in the spectrum lies in one bin. For the last N-1 samples in Figure 2, leakage occurs again, and the spectral energy decays to zero.

In Figure 3, an example of speech analysis is given. An 72-point DFT is used, and the MFTs are spaced by 14 samples. The speech is a 0.275 s record of the word "pipe".

Figure 3: Speech analysis using the MFT

Consider the case where N-point DFTs are used to analyze an N_u-point complex-valued data record. If the input data is shifted by q samples between each DFT application, where , then DFTs are needed to spectrum analyze the record. It is assumed that the coefficients are precomputed and stored.

Then, when radix-2 FFTs are used to analyze the data,

real operations (20)

are needed. It can be shown that in the case of the MFT, the number of real operations needed are:

(21)

where N₁ is the number of DFT coefficients that are to be computed, .

Figure 4: Comparison of MFT and FFT arithmetic.

This computing load is illustrated in Figure 4, for the case of N_u = 1024, N = 64, and N₁ = 4 & 64. The FFT is quite efficient if the shift increment q > N / 4, but is very inefficient if the shift between FFTs is only a few samples. In contrast, the MFT is very efficient compared to the FFT if the shift between samples is small, but its relative efficiency drops as the shift q increases. The efficiencies of the FFT and the full MFT are approximately the same when q = 4. However, if only a few DFT coefficients are needed (e.g. N₁ = 4), the reduced MFT is very efficient, even for large values of shift between DFTs. Similar conclusions are reached with different values of N and N_u. Note also that:

1. The MFT efficiency curves of Figure 4 are flat because the operations are proportional to q. This means that the DFT of every sample shift can be computed with no further overhead, if desired.
2. The MFT does not rely upon N being a power of two to obtain its efficiency.
3. When the input data is real-valued, the comparison of efficiencies is similar, as long as steps are taken to eliminate the unnecessary operations in each case.
4. Weighting or window functions can be included in the MFT application, although not as simply as in the case of the FFT [5].

As a second example of efficiency, consider an N-point frequency domain filter applied with a fast convolution. The filter is applied with a forward FFT (or MFT), an array multiply, then an inverse FFT (or MFT). The comparison of efficiencies is shown in Figure 5. If the full MFT is used to compute all the DFT coefficients, then the FFT is more efficient. But if only a subset of the DFT coefficients need be computed, the MFT/IMFT option can be more efficient for many values of N.

Figure 5: Efficiency comparison in fast convolution

6. CONCLUSIONS

The momentary or moving Fourier transform has been derived using a matrix formulation of the DFT, and an incremental form has also been given. The incremental or recursive form is particularly efficient when successive DFTs with a high overlap ratio is to be computed, or when only a few DFT coefficients are needed. Recursive and non-recursive inverse MFTs have also been derived, including a non-recursive form which requires only additions to obtain the time sequence.

ACKNOWLEDGEMENTS

The authors would like to thank Dr. József Dúdás for introducing them to the momentary Fourier transform. Financial support from the NSERC/MDA Industrial Research Chair in Radar Remote Sensing is gratefully acknowledged.

REFERENCES

[1] A. Papoulis, Signal Analysis. McGraw-Hill, 1977

[2] R. R. Bitmead and C. D. O. Anderson, "Adaptive frequenct sampling filters," IEEE Trans. On Circuits and Systems, vol. CAS-28, pp. 524-534, June 1981.

[3] J. Dúdás, The Momentary Fourier Transform. PhD thesis, Technical University of Budapest, 1986.

[4] J. H. Lilly, "Efficient DFT-based model reduction for continuous systems," IEEE Trans. On Automatic Control, vol. 36, pp. 1188-1193, Oct. 1991

[5] B. G. Sherlock and D. M. Monro, "Moving discrete Fourier transform," IEE Proceedings-F, vol. 139, pp. 279-282, Aug. 1992.

Last updated: 27^th March 1998 by Ian Cumming.