Analysis and Precision Processing of RADARSAT ScanSAR Data
Ian Cumming and Yi Guo
Dept. of Electrical and Computer Engineering
The University of British Columbia
Vancouver, BC, Canada V6T 1Z4.
ianc@ee.ubc.ca yig@ee.ubc.ca
http://www.ee.ubc/sar/
Frank Wong
MacDonald Dettwiler and Associates
Richmond, BC, Canada V6V 2J3.
ABSTRACT
RADARSAT ScanSAR data is obtained using burst-mode operation, which records data with a discontinuous Doppler spectrum. When ScanSAR data is used in SAR interferometry, the compression algorithms have to be phase preserving. Single burst data can be compressed by an ideal but target-dependent matched filter, or by a practical and target-independent matched filter. Bamler's algorithm and short IFFT algorithm are phase preserving compression algorithms based on the practical compression method and we show how these two algorithms produce different compressed results.
1. Introduction
Quite a few papers have been published in the last several years on phase preserving SAR processing algorithms, including the classical range/Doppler, modified range/Doppler, SPECAN (de-ramp and FFT), and chirp scaling. These algorithms work well on continuous-mode SAR data, such as Radarsat's regular beams, but must be modified when applied to burst-mode data, such as Radarsat's ScanSAR modes. This is because the spectrum of the data collected in burst-mode varies with time.
With the recent interest in interferometry, it is important that SAR processing algorithms be phase preserving [1]. However, the time-varying spectrum of burst-mode data inherently introduces phase variations, and special modifications must be made to the processing algorithms to regain the correct phase properties of the received data. This paper will discuss the phase properties of burst-mode data, and possible algorithms for phase preserving processing RADARSAT ScanSAR data.
This paper will introduce Radarsatís ScanSAR mode of operation [2], and will analyze the properties of burst-mode data by comparing them to the continuous SAR data. The phase preserving compression methods for one block burst data are discussed in the third section, in which the "ideal" compression and "practical" compression methods are analyzed. In section four, phase preserving compression algorithms for point target burst-mode data will be compared and discussed.
2. ScanSAR operating mode and its data properties
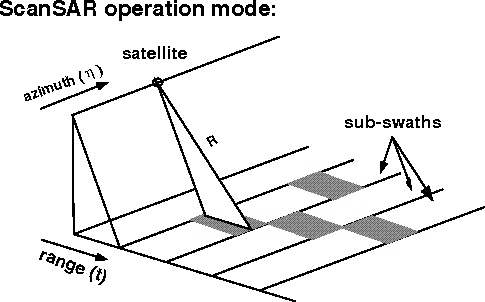
When SAR works in a continuous mode, the radar beam scans through only one range swath on the earthís surface, while in a ScanSAR mode, the beam scans one subswath for a certain period, and then jumps to the next subswath, so that it has much wider imaged swath than a conventional SAR. Fig. 1 shows this ScanSAR operating mode and the subswaths.

Figure 1 The ScanSAR operation mode.
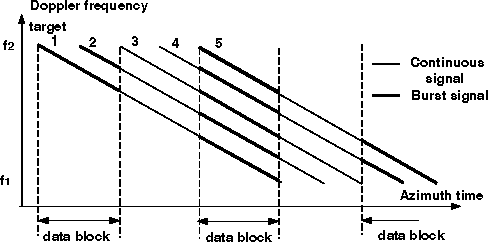
Figure 2 Comparison of target Doppler frequency between continuous and burst mode.
If we examine only one subswath at a time, the data in the range direction has the same properties as that of the continuous mode. But in the azimuth direction, the data in this subswath is discontinuous, and is equivalent to data truncated from continuous-mode azimuth data. Ignoring the azimuth antenna pattern, the two-dimensional burst-mode received signal can be expressed as follows:
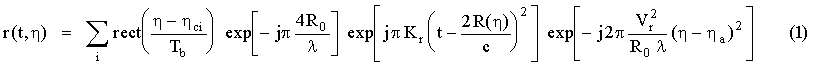
Here R(h ) is the distance between the satellite antenna and the target at azimuth time h , t is the range time, and R0 is the range of closest approach which occurs at azimuth time h a. Kr is the range FM rate, Vr is the speed of the satellite in the azimuth direction, and f0 the radar carrier frequency. Each burst block has a length of Tb, and the center time of the ith burst is h ci. The wavelength of the radar is l , and c is the radar propagation speed. The first phase term describes the unique distance of the target to the satellite orbit, which is the information to be preserved for SAR interferometry processing.
The comparison of burst-mode data and continuous-mode data can be illustrated by a sketch of the Doppler frequency versus azimuth time of five targets, as shown in Fig. 2. In this figure, the continuous data covers the same Doppler bandwidth for each target from f1 to f2. Burst-mode data, on the other hand, is collected in blocks, and each target has a different, segmented Doppler spectrum, dependent upon its azimuth position.
This segmented Doppler spectrum of burst-mode data makes it difficult to apply traditional matched filtering compression methods. In the traditional continuous case, all the targets with the same Doppler bandwidth can be compressed by a target-independent matched filter. The compressed targets have the same phase slope, and the phase p 4R0/l is preserved at the peaks. However, in the burst-mode case, different targets have different burst spectral distributions, and directly applying a traditional match filtering compression method will end up with more complicated results, as explained in the following sections.
3. Compression of a single burst
Since the range signal in burst-mode data is the same as that of the continuous data, this paper focuses on azimuth compression only. We begin by examining the compression methods of a single burst of data.
3.1 Ideal compression of one burst
Ignoring the phase item exp[j4p R0/ l ], a point target within one single burst can be expressed as:
![]()
where Ka is the azimuth FM rate Vr2/(R0
l ), and h cb
is the center of the burst. The ideal compression of this target is achieved
by a matched filter which is the time reversed complex conjugate of this
data with the same time duration. Therefore the phase of the compressed
signal will have the same properties as that of the compressed continuous
data, in which the linear phase ramp has a slope proportional to the center
frequency of the signal, and at the peak, the phase is zero. However, the
compressed phase slope will change when the burst center frequency changes.
As an example, the ideal compression result of a target with zero burst
center frequency is shown in Fig. 3.
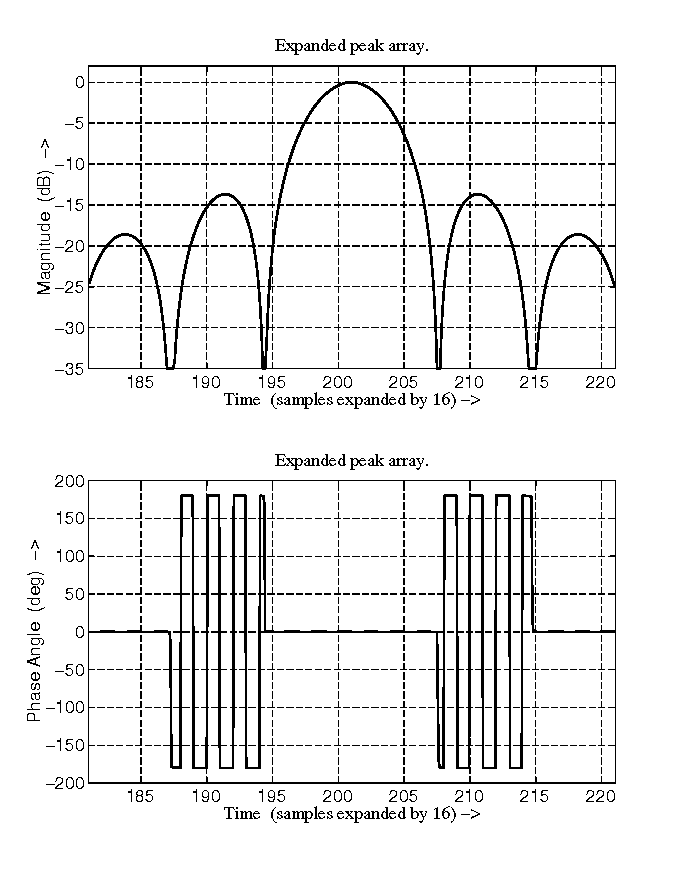
Figure 3 The ideal compression result of a single burst (ISLR=-11.0 dB).
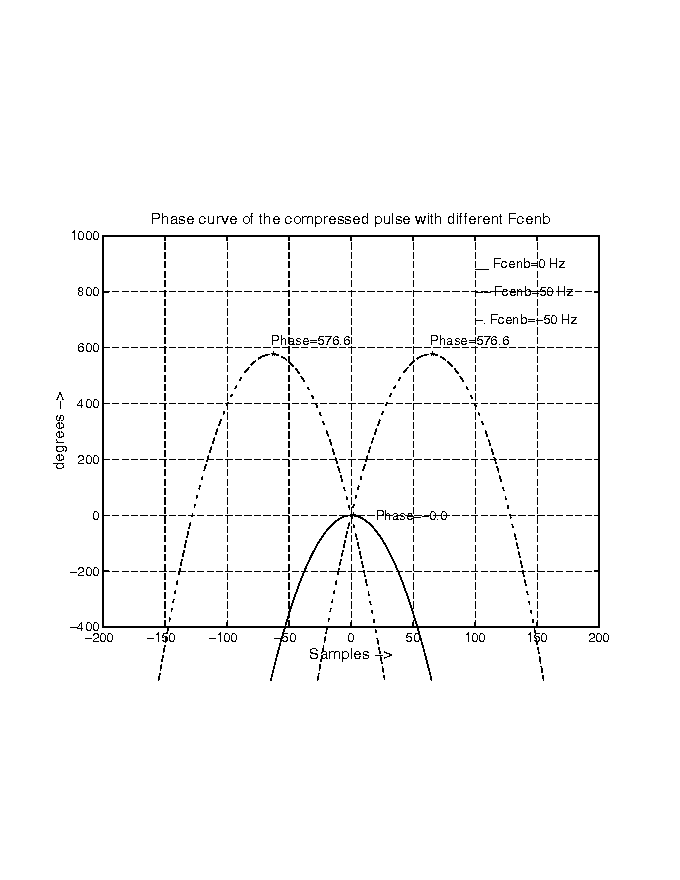
Figure 4 The phase curve of the practical compressed pulse with different Fcenb
In real data, each burst will capture signals from many different targets, and these signals cover different extents of the Doppler spectrum. In other words, in one burst, different targets have different center frequencies, so for this ideal compression, the matched filter must be target dependent in order to compress and separate signals from different targets. Practically speaking, this ideal compression is very time consuming to apply. However, studying the ideal compression can tell us what the phase of the compressed pulse should be, so that the results from the practical compression can be compared with the ideal result.
3.2 Practical compression of one burst
In order to develop an efficient compression scheme, a matched filter should be developed which compresses all the targets in each burst with a single convolution operation. To do this, the matched filter must encompass all the possible target frequencies, which are the same range of frequencies that are present in the continuous-mode case. Thus the matched filter is the same matched filter as in the continuous mode. If a full-aperture azimuth signal is:
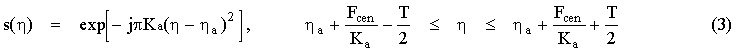
where T is the length of the aperture, and Fcen is the Doppler centroid frequency. Then, setting h a = 0, the full-aperture matched filter is m(h ) = s*(-h ). The compressed data c(h ) will be:
![]()
where h 1 = (h cb-Tb/2) , h 2 = h cb+Tb/2, and h cb-Tb/2 £ h £ T- (h cb+Tb/2 ).
In this practical compression, the pulse is compressed to a sinc
function, but the phase
p [-Ka (h
-h a)2 + 2 Fcenb(h
-h a)] now has a small quadratic
component as well as the familiar linear component. This quadratic phase
is zero at the peak (when h =h
a). The shape (i.e. second derivative) of the phase curve
depends only upon Ka, but the position changes when Fcenb
changes.
Fig. 4 shows how the position of the phase curve changes when different values of Fcenb are used. Note that the phase goes through zero at the peak position (sample number zero). It also shows that when Fcenb = 0, the phase change around the peak will be very small, and when Fcenb increases, the phase change will be larger in the main lobe.
In the simulation of the practical compression, two different values of Fcenb (0 Hz and 11 Hz) are used. The compressed peaks are shown in Fig. 5 and Fig. 6. It can be seen that when the burst center frequency moves to a different location, the compressed phase curve changes to a different part of the quadratic curve. The phase at the peak of the compressed pulse is always zero.
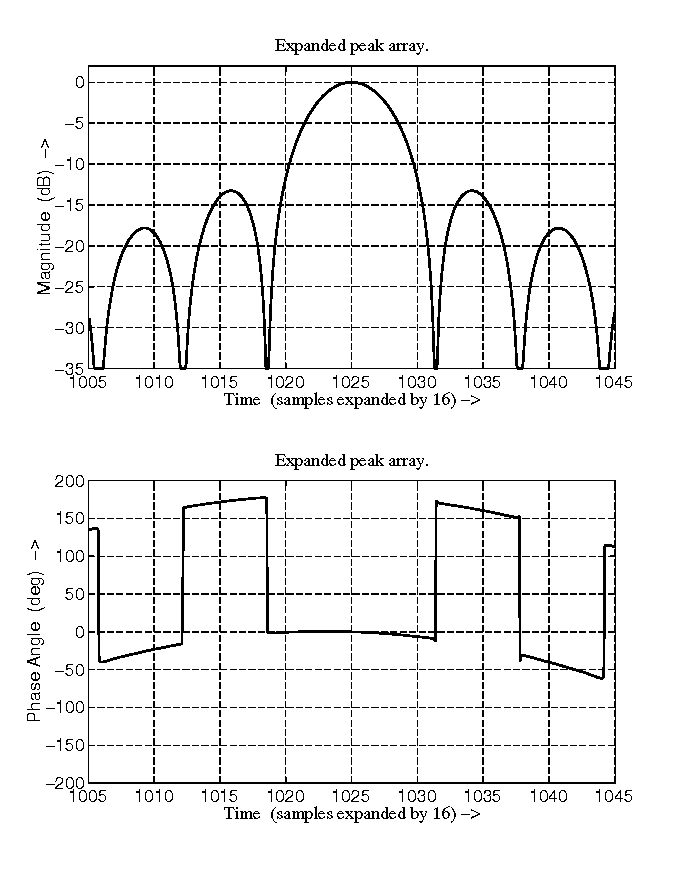
Figure 5 The practical compressed pulse when Fcenb = 0 Hz (ISLR= - 10.2 dB)
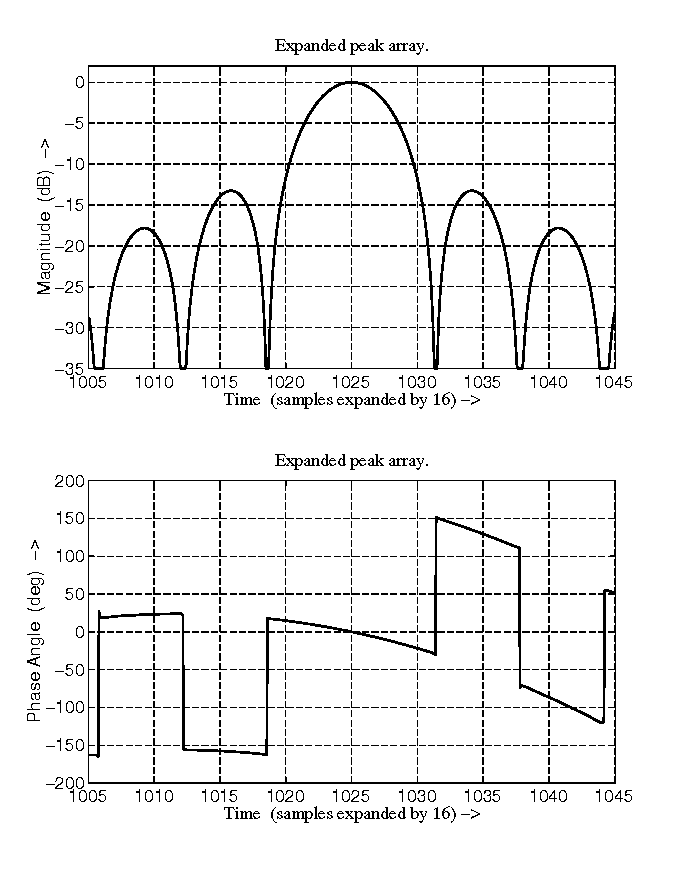
Figure 6 The practical compressed pulse when Fcenb=11 Hz
From the above analysis, we can conclude that the practical compression of a single block of burst-mode data is achieved with a target-independent matched filter. It compresses into a sinc function with zero phase at the peak, and a burst-dependent quadratic phase curve through the pulse.
3.3 Signal noise ratio considerations
When the signal noise ratio (SNR) is taken into account, one disadvantage of the practical compression is that it has lower SNR compared with the ideal compression. The reason is that, when full bandwidth receiver noise is mixed in the signal, the long practical matched filter will pass through more noise than the short ideal matched filter, according to the ratio of their bandwidths.
As a simple simulation example, we add a "noise" which is a random value throughout the Doppler spectrum, at a level of 1/100 of the signal magnitude. The burst data is captured at the center of the aperture with a center frequency of zero. The compressed pulses using ideal compression and practical compression are shown in Fig. 7(a) and (b).
Compared to the case without noise (Fig. 3 and Fig. 5) the integrated side lobe ratio (ISLR) experiences the most change. In Fig. 7, the ISLR of the ideal compression is much lower than the practical case. Also the ideal compression result has a better shape than the practical compression result (specially the phase inside the main lobe which has less noise).
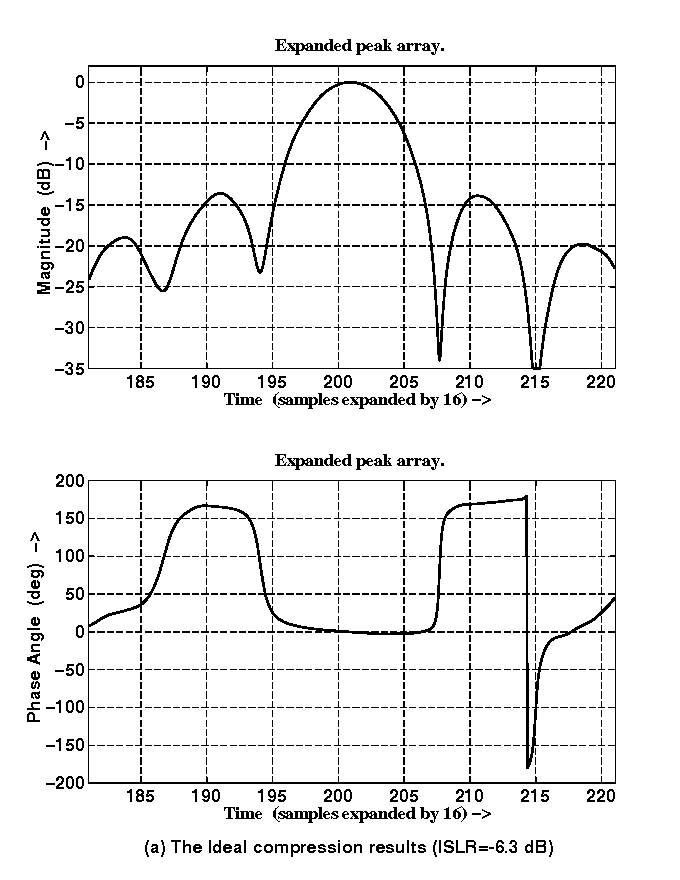
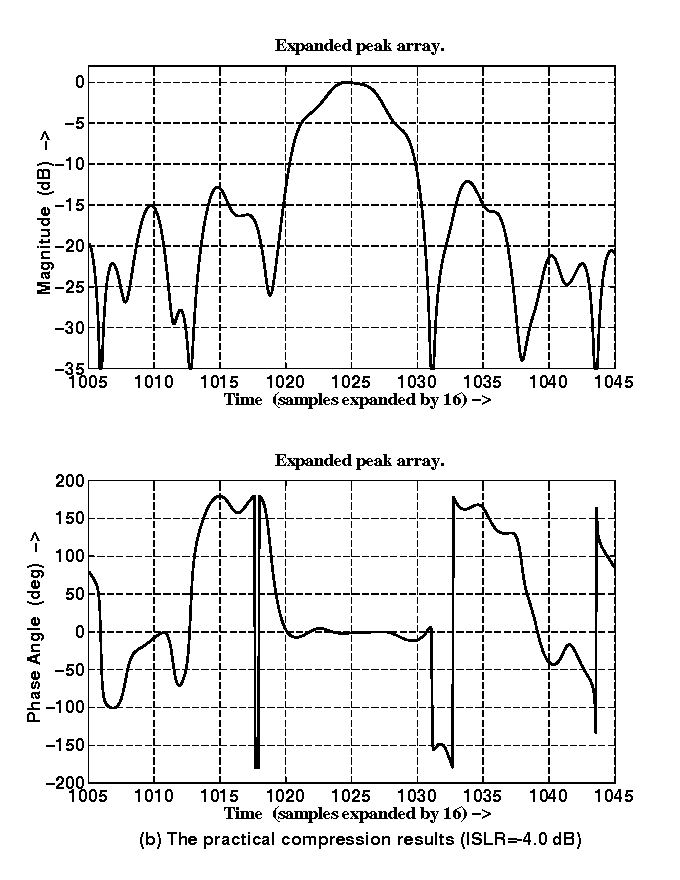
Figure 7 Comparison of SNRs between ideal and practical compression methods
3.4 Discussion
In the analysis of this section, we see that the ideal compression of the burst-mode data is target dependent, because of the different Doppler extent of each target. However, it is not efficient to apply the ideal matched filter, because a different matched filter has to be designed for each output sample, and the efficiency of the fast convolution using FFTs cannot be obtained.
On the other hand, an efficient matched filter can be obtained by using the same long matched filter as we would for continuous-mode SAR data. We call this the "practical" matched filter because of its efficiency. This practical matched filter gives nearly target-independent compression, and the phase of the compressed pulse has the correct value of zero at the middle of the peak.
However, the practical matched filter has two disadvantages compared with the ideal matched filter. Firstly, the compressed phase has a small quadratic component, which gives the average phase throughout the main lobe a small negative bias. The ideal compression has a linear phase throughout the main lobe, so that the average main lobe phase is zero. But the quadratic component gives a bias of up to 2o, which represents a small phase error, and can be ignored.
Secondly, the practical compression has a worse signal/noise ratio, by a factor equal to the ratio of the lengths of the long vs. the short (ideal) matched filters. The SNR reduction equals the aperture length divided by the burst length, which can be in the order of 2 - 10, a significant amount.
For interferometry applications, the phase bias may be of no consequence, as it is small, and will cancel out if the bursts are aligned in the two scenes. The bursts have to be fairly well aligned for interferometry to work, else the two images will not have enough correlation. However, the signal/noise issue might be important, as satellite interferometry suffers from marginal SNR at the best of times in continuous mode. In burst mode, the processing is more critical because of the smaller bandwidth used, so the extra noise introduced by the practical matched filter may not be acceptable.
4 Compression of point target burst-mode data
Based on the foregoing discussion, two methods of point target burst mode compression can be evaluated.
4.1 Bamler's algorithm
Bamler's algorithm [3] is based on the range/Doppler algorithm. By padding zeros in the burst gaps, it processes all the bursts at once using a full-aperture matched filter. Therefore, the compression algorithm is similar to that of the continuous case, and includes the following steps:
In the last processing step, the azimuth processing uses a full aperture matched filter to compress the burst spectra. Since each target may exist in more than one block of burst data, the compression here is different from the practical compression; however, it can be viewed as processing each burst individually and then summing the results. As concluded in the previous section, the compressed phase slope of a point target in each individually-processed burst is proportional to the burst center location. When several such pulses are added together, different phase slopes will give spikes in the summation output, as shown in Fig. 8 where 2 bursts per aperture are simulated. Another point of view is that the spikes are caused by the rectangular modulation of the data due to the intermittent data collection. However, the peak phase of the compressed pulse is zero, which means phase is preserved at the peak.
Fig. 9 shows the two dimensional compression of a point target using Bamler's algorithm. In the azimuth direction, the spikes are very obvious.
4.2 Short IFFT (SIFFT) algorithm
Processing all the bursts in one step requires only one target-independent matched filter, but gives a spiky compressed pulse. In contrast, compressing one burst for each target can avoid the spikes, but usually needs a target-dependent matched filter. The SIFFT algorithm [4], a compression algorithm using one burst block for each target, avoids the spikes yet uses a target-independent matched filter.
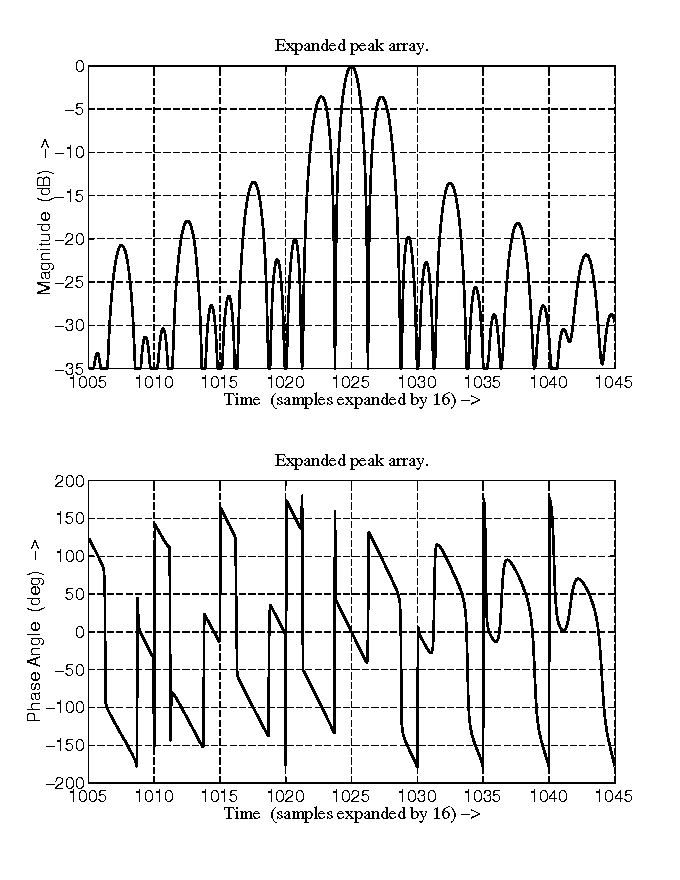
Figure 8 The compressed result by Bamler's algorithm.
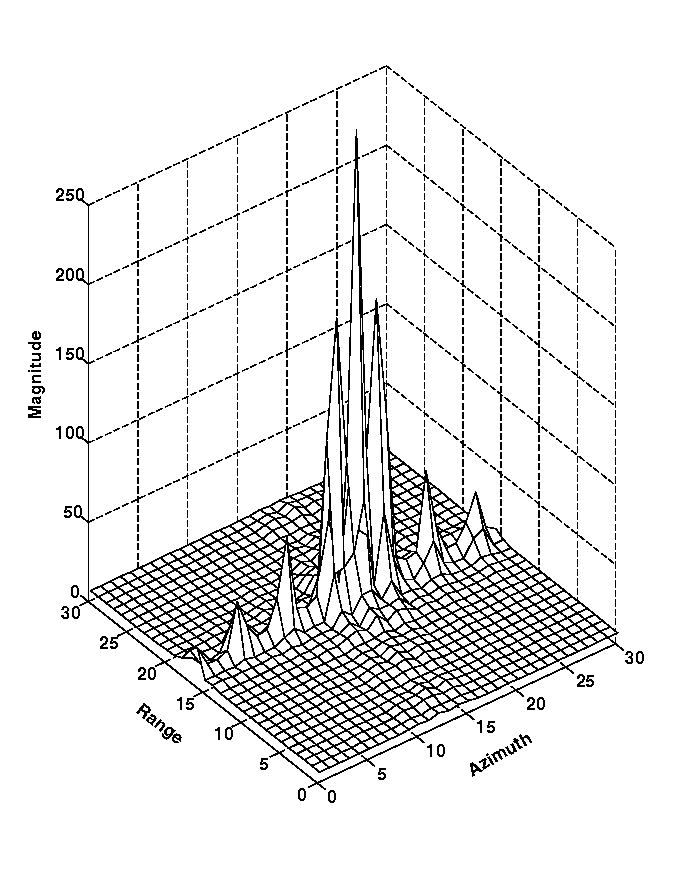
Figure 9 The 2-D compression of a point target by Bamler's algorithm.
The SIFFT algorithm differs from Bamler's method in the azimuth IFFT step, where only a part of the spectrum is taken for each IFFT, and the compressed pulses from several such short IFFTs will be stitched together to obtain the compression of all the targets. The IFFT length is made short enough so that only the energy of one burst is captured by each IFFT. In effect, the IFFTs behave like time-varying bandpass filters.
This algorithm is in between the ideal compression and practical compression, since the compressed pulse of a target comes from the spectrum of one block of data and the full aperture matched filter is target independent. The resolution of the SIFFT output is governed by the bandwidth of the single burst spectrum.
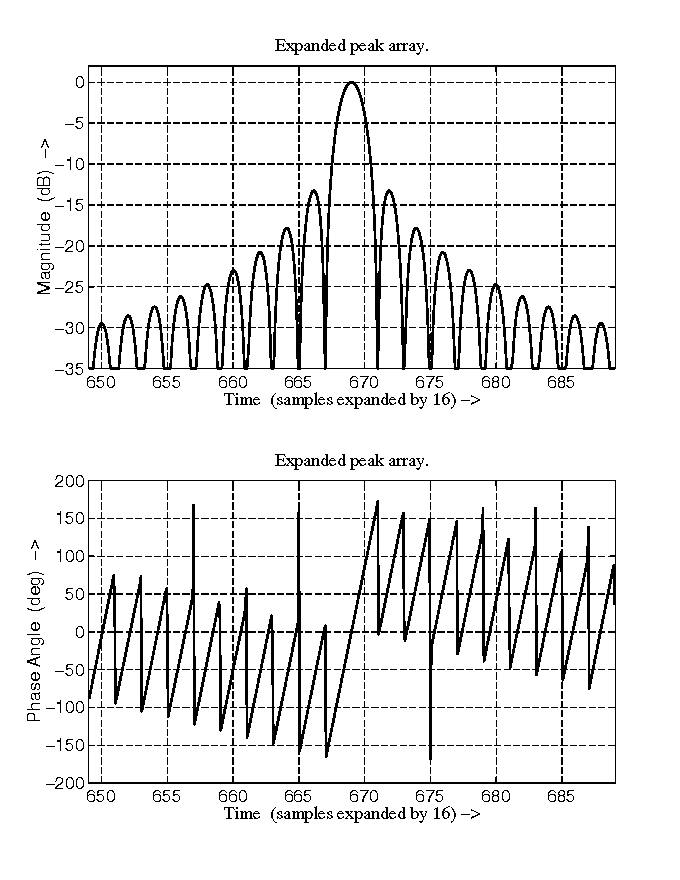
Figure 10 compressed pulse using SIFFT.
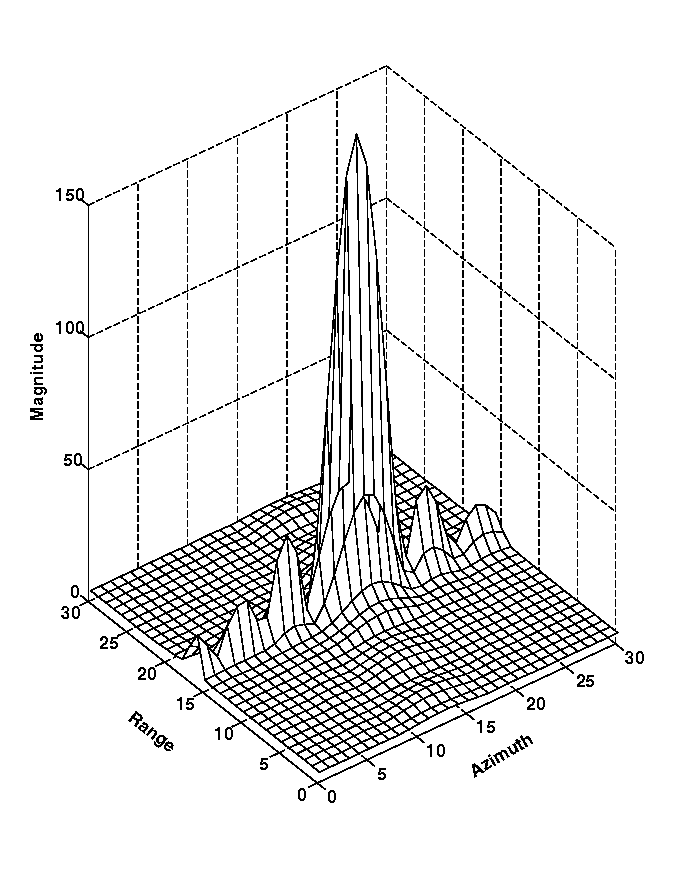
Figure 11 The 2-D compression using SIFFT.
Fig. 10 shows the magnitude and phase of the compressed pulse. In the phase curve, the phase is zero at the peak, and the phase slope is proportional to the center frequency of the burst. Fig. 11 shows the 2-dimensional compression of a point target using the SIFFT algorithm.
4.3 Discussion
These two algorithms for burst-mode data compression are both phase preserving at the peak of the compressed pulse. Using more than one burst in Bamler's algorithm, the compressed pulse is spiky and these spikes may introduce extra noise in the InSAR processing.
The SIFFT algorithm has a better compressed pulse shape than Bamler's algorithm. However, stitching of the compressed pulse will create a discontinuous phase in some targets, and this might influence the InSAR results. This effect is currently under investigation.
4.3 Conclusions
ScanSAR burst-mode data has been analyzed, and its discontinuous Doppler spectrum requires a new algorithm for phase preserving processing in the azimuth direction. Single burst compression shows that the ideal compression gives a linear phase throughout the compressed pulse, and preserves the phase at the peak of the pulse. However, this compression is target dependent, and not efficient for real data. The practical compression of a single burst is target independent, preserves phase at the peak, but generates a small quadratic phase curve throughout the pulse.
For phase preserving algorithms of point target data, both Bamler's algorithm and the SIFFT algorithm preserve the phase at the peak of the compressed pulse. Bamler's result is spiky, while the compressed pulse from SIFFT algorithm has phase discontinuity problem at some stitching points.
Acknowledgments
Financial support from NSERC, BCASI, BCSC and MacDonald Dettwiler is gratefully acknowledged.
References
[1] E. Rodriguez and J. Martin, Satellite Interferometer Radar for Topographic Mapping, IEE Proceedings-F, Vol. 139, pp.147-159, 1992.
[2] A. P. Luscombe, I. Ferguson, N. Shepherd, D. Zimcik, and P. Naraine, The RADARSAT Synthetic Aperture Radar Development, Canadian Journal of Remote Sensing, Vol. 19, No. 4, pp. 289 - 310, 1993.
[3] R. Bamler and M. Eineder, ScanSAR Processing Using Standard High Precision SAR Algorithms, IEEE Trans. On Geosci. and Remote Sensing, Vol. 34, No. 1, Jan. 1996.
[4] F. Wong, D. Stevens and I. Cumming, Phase-Preserving Processing of ScanSAR Data with a Modified Range-Doppler Algorithm, to be presented at IGARSSí97, Singapore, Aug. 4-8, 1997.